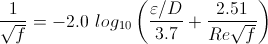
Colebrook equation
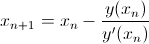
Newton's method
The Moody chart is based on the solutions to the Colebrook equation; this calculator uses Newton's method for finding zeros to solve the Colebrook equation.
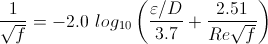 Colebrook equation |
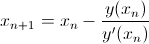 Newton's method |
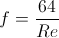 Friction factor for laminar flow |
Fully rough flow is when increasing the Reynolds number of a turbulent flow no longer affects the friction factor. Unlike laminar flow, the friction factor of fully rough flow depends only on the relative roughness of a pipe. In this case the friction factor can be expressed explicitly as a function of relative roughness using the von Kármán equation. For convenience, a variable x will be defined as the inverse square root of the friction factor, and this will be used for the remainder of this explanation.
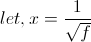 |
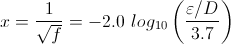 von Kármán equation for fully rough flow |
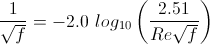 Prandtl equation
|
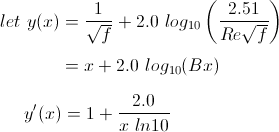 Form of Prandtl equation for Newton's method |
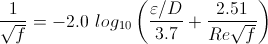 Colebrook equation
|
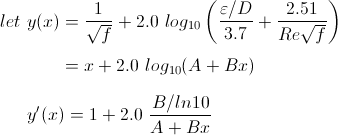 Form of Colebrook equation for Newton's method |
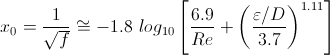 S. H. Haaland relationship
|
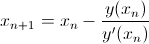 Newton's method
|
function moody(Re (Reynolds Number),
rel_e (Relative roughness (e/D)),
n (iterations (optional)))
begin
if Re = 0 (no flow) then
return "infinity"
if Re <=2300 (Laminar Flow condition) then
return 64/Re;
if Re < 4000 (Transition Flow, this cannot be accurately calculated) then
return "transition flow"
(Turbulent Flow conditions)
var x (x = f^(-1/2))
if Re = Infinity (fully rough flow) then
begin
if rel_e = 0 then
return 0
else
x=-2.0*log10(rel_e/3.7) (Von Karman equation)
return 1/(x^2) (f = 1/x^2)
end
equation y (y = 0, this is used in Newton's method to find x),
y' (y'= dy/dx)
var A (A = (e/D)/3.7),
B (B = 2.51/Re )
B = 2.51/Re
if rel_e = 0 (smooth pipe flow) then
begin
A = 0
y(x) = "x+2*log10(B*x)" (y = Prandtl equation = 0)
y'(x) = "1+2/(x*ln10)"
end
else if rel_e > 0 (typical turbulent pipe flow) then
begin
A = rel_e/3.7
y(x) = "x+2*log10(A+B*x)" (y = Colebrook equation =0)
y'(x) = "1+2*(B/ln10)/(A+B*x)"
end
if n is undefined then
n = 3 (default # of iterations for Newton's Method)
x = -1.8*log10((6.9/Re)+A^1.11) (S.E. Haaland equation (initial guess))
for var i from 1 to n (Newton's Method)
x = x-y(x)/y'(x)
return 1/(x^2) (f = 1/x^2)
end
|
It is important to recognize the code above requires the ability to evaluate a string as an equation. This is not convenient to do in most programming languages. Also for real world situations (i.e. 0<Re<∞ and 0≤ε/D<1) the friction factor only needs to be evaluated from the laminar flow relationship or Colebrook equation. I only added these other cases for completeness, but the pseudocode above can be simplified to the pseudocode below for simple accurate real world calculations.
function moody(Re (Reynolds Number),
rel_e (Relative roughness (e/D)),
n (iterations (optional)))
begin
if Re <=2300 (Laminar Flow) then
return 64/Re;
if Re < 4000 (Transition Flow, this cannot be accurately calculated) then
return "transition flow"
(Turbulent Flow)
var x (x = f^(-1/2)),
y (y = 0, this is used in Newton's method to find x),
y' (y'= dy/dx),
A (A = (e/D)/3.7),
B (B = 2.51/Re )
A = rel_e/3.7
B = 2.51/Re
if n is undefined then
n = 3 (default # of iterations for Newton's Method)
x = -1.8*log10((6.9/Re)+A^1.11) (S.E. Haaland equation (initial guess))
for var i from 1 to n (Newton's Method)
begin
y = x+2*log10(A+B*x) (y = Colebrook equation =0)
y' = 1+2*(B/ln10)/(A+B*x)
x = x - y/y'
end
return 1/(x^2) (f = 1/x^2)
end
|
If you have any questions, comments, or concerns I can be contacted at michael.r.maley@gmail.com.